밑바닥부터 시작하는 딥러닝 - 2 퍼셉트론

Chapter 2 퍼셉트론

2.1 퍼셉트론이란?

• 뇌의 뉴런과 마찬가지로 입력을 받아서 뉴런의 공식에 따라서 출력 신호를 내보낸다.
• 이 장에서 설명하는 퍼셉트론은 입력을 받아 출력을 한다 (1), 안한다 (0)으로만 한다고 가정
• 입력신호노드에서 출력 신호 노드로 신호가 보내질 때 각각 고유의 가중치 W 가 존재함
• 예를 들어, 입력이 X₁, X₂ 이고, 각 입력에 대한 가중치가 W₁, W₂ 이고, 출력을 위한 임계치가 \theta 일때,
• y = 0 if X₁W₁, X₂W₂ <= \theta, else 1 로 정의할 수 있다.

2.2 단순한 논리 회로

• AND, OR, NAND 등의 논리 게이트에 대한 진리표를 바탕으로 가중치와 임계치를 정의할 수 있다.
• 예를 들어 OR 게이트의 가중치는 (1, 1, 1), (0,5, 0.5, 0.5) 등 무한하게 정의 할 수 있다.
• 여기서 퍼셉트론의 매개변수 (가중치와 임계치 \theta)를 정의하는 것은 사람이다.
• 학습 을 통해서 적절한 매개변수 값을 정할 수 있으며 사람이 매개변수를 정의하는 모델을 고민하여 컴퓨터에 학습을 수행할 데이터를 주는 일을 한다.

2.3 퍼셉트론 구현하기

2.3.1 단순 논리 게이트 회로 만들기

• AND 게이트는 아래와 같이 매우 간단하게 작성할 수 있다.

def AND(x1, x2):
  w1, w2, theta = 0.5, 0.5, 0.7
  tmp = x1 * w1 + x2 * w2
  if tmp <= theta:
    return 0
  else:
    return 1

2.3.2 가중치와 편향 도입

• 앞서 정의했던 가중치 \theta를 조금 바구면 다시 식을 작성할 수 있는데, 이때 \theta를 b (bias, 편향)로 다시 정의해보자.
• y = 0 if b + X₁W₁, X₂W₂ <= 0, else 1
• 식을 해석해보면 bias b 값을 입력 신호와 더하여 0보다 넘으면 1을 출력하도록 한다.

2.3.3 가중치와 편향을 도입한 AND 게이트

import numpy as np

def AND(x1, x2):
  x = np.array([x1, x2])
  w = np.array([0.5, 0.5])
  b = -0.7
  tmp = np.sum(w*x) + b # numpy array multiply is elementwise if number of elements between two array is same
  if tmp <= 0:
    return 0
  else:
    return 1

• 가중치는 입력 신호에 영향력 (중요도)를 조절하는 요소
• 편향은 노드가 얼마나 쉽게 활성화 될 수 있도록 하느냐를 조절하는 요소
• NAND 게이트는 아래와 같이 구할 수 있다.

import numpy as np

def NAND(x1, x2):
  x = np.array([x1, x2])
  w = np.array([-0.5, -0.5]) # Only weight and bias are different
  b = 0.7
  tmp = np.sum(w*x) + b
  if tmp <= 0:
    return 0
  else:
    return 1

• 코드를 통해 알 수 있듯이 가중치와 편향 값만 조절하여 게이트의 성격을 바꿀 수 있다.

2.4 퍼셉트론의 한계

2.4.1 XOR 논리 게이트

• XOR는 서로 다른 값이 입력으로 들어 왔을 때만 출력이 1이 되는 논리게이트 이다.
• 예를 들어 OR 게이트는 y = -0.5 +X₁ + X₂ 로 간단히 표현할 수 있다. (가중치 1, bias -0.5) 이때 그어지는 1차 함수 직선 아래는 0으로 위는 1로 간주할 수 있다.
• XOR 게이트는 이와 같이 직선으로 나타내거나 일정한 수식으로 나타내기가 어렵다. (직선 하나로 나누기란 불가능하다)

2.4.2 선형과 비선형

• 단 곡선으로 나눈다면 어떻게 영역 표시를 할 수는 있다.
• 문제는 그렇게 스바라시한 곡선을 표현하기는 어렵다는 것이다.
• OR 게이트의 수식과 같이 직선으로 표현이 가능한 영역을 선형, 곡선으로 표현이 가능한 영역을 비선형 으로 정의한다.

2.5 다층 퍼셉트론이 출동한다면

• 1개의 퍼셉트론으로는 XOR 게이트를 표현할 수 없었다.
• 하지만 여러개의 퍼셉트론을 쌓아서 시도해 볼 수 있다.
• 여러개의 퍼셉트론이 개층으로 쌓인 전체 퍼셉트론을 다층 퍼셉트론 (multi-layer perceptron)으로 정의한다.

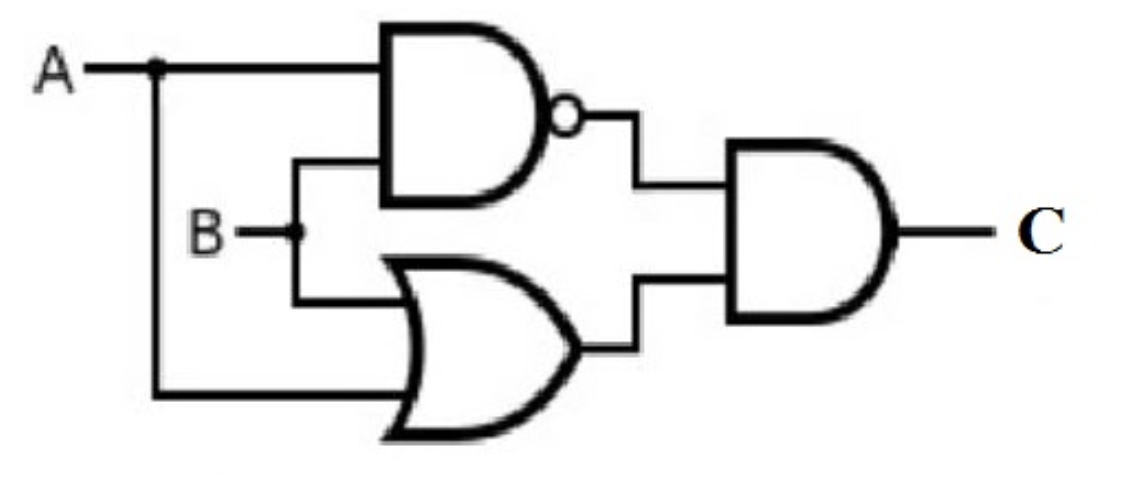
• 위와 같이 XOR 게이트도 여러개의 게이트를 조합해서 구현이 가능하다.

import numpy as np

def AND(x1, x2):
  x = np.array([x1, x2])
  w = np.array([0.5, 0.5])
  b = -0.7
  tmp = np.sum(w*x) + b # numpy array multiply is elementwise if number of elements between two array is same
  if tmp <= 0:
    return 0
  else:
    return 1

def NAND(x1, x2):
  x = np.array([x1, x2])
  w = np.array([-0.5, -0.5]) # Only weight and bias are different
  b = 0.7
  tmp = np.sum(w*x) + b
  if tmp <= 0:
    return 0
  else:
    return 1
  
def OR(x1, x2):
  x = np.array([x1, x2])
  w = np.array([0.5, 0.5]) # Only weight and bias are different
  b = 0.5
  tmp = np.sum(w*x) + b
  if tmp <= 0:
    return 0
  else:
    return 1
  
def XOR(x1, x2):
  S1 = NAND(x1, x2)
  S2 = OR(x1, x2)
  return AND(S1, S2)

• XOR 함수에서 입력 받은 x1, x2를 다층 레이어 퍼셉트론의 0층이라고 하며, S1, S2를 1층 마지막 결과를 2층으로 차례대로 계층화 할 수 있다.
• 0층의 신호가 개개의 퍼셉트론을 거쳐서 1층으로 전달되고, 1층 퍼셉트론을 거친 값들이 2층의 퍼셉트론으로 전달되어 결과 값을 얻는 방식이다.
• 이처럼 단층 퍼셉트론으로 표현할 수 없는 비선형적 내용들을 여러개의 개층으로 쌓아서 표현해 낼 수 있다.

2.6 NAND에서 컴퓨터까지

• 위처럼 여러개의 퍼셉트론을 통해서 표현하면 복잡한 회로를 만들 수 있다.
• 이론적으로 NAND게이트로 컴퓨터를 만들 수 있으니, 다층 퍼셉트론으로 컴퓨터를 만들 수 있다라는 의미도 된다!
• 그러나 복잡한 일을 수행하는 퍼셉트론을 만들려면 가중치와 편향 값을 잘 조절해야하는 문제가 발생한다.
• 여러개의 간단한 퍼셉트론을 모듈화 해서 만든 다음 조립하는 방식이 합리적이다.